Conjugate Direction Methods
Code
Please visit this page for a code implementation of the conjugate gradiant method.
Conjugate Direction Methods
The class of conjugate direction methods can be viewed as being intermediate between the method of steepest descent and Newton's method. The conjugate direction methods have the following properties:
- Solve quadratics of n variables in n steps.
- The usual implementation, the conjugate gradient algorithm, requires no Hessian matrix evaluations.
- No matrix inversion and no storage of an n×n matrix are required.
The conjugate direction methods typically perform better than the method of steepest descent, but not as well as Newton's method. As we saw from the method of steepest descent and Newton's method, the crucial factor in the efficiency of an iterative search method is the direction of search at each iteration. For a quadratic function of n variables f(x)=21x⊤Qx−x⊤b, x∈Rn,Q=Q⊤>0, the best direction of search, as we shall see, is in the Q-conjugate direction. Basically, two directions d(1) and d(2) in Rn are said to be Q-conjugate if d(1)⊤Qd(2)=0. In general, we have the following definition.
Definition
Let Q be a real symmetric n×n matrix. The directions d(0),d(1),d(2),…,d(m) are Q-conjugate if for all i=j, we have d(i)⊤Qd(j)= 0.
Lemma 1
Let Q be a symmetric positive definite n×n matrix. If the directions d(0),d(1),…,d(k)∈Rn,k≤n−1, are nonzero and Q-conjugate, then they are linearly independent.
Proof
Let α0,…,αk be scalars such that
α0d(0)+α1d(1)+⋯+αkd(k)=0. Premultiplying this equality by d(j)⊤Q,0≤j≤k, yields
αjd(j)⊤Qd(j)=0, because all other terms d(j)⊤Qd(i)=0,i=j, by Q-conjugacy. But Q=Q⊤>0 and d(j)=0; hence αj=0,j=0,1,…,k. Therefore, d(0),d(1),…,d(k),k≤n−1, are linearly independent.
The Conjugate Direction Algorithm
We now present the conjugate direction algorithm for minimizing the quadratic function of n variables
f(x)=21x⊤Qx−x⊤b, where Q=Q⊤>0,x∈Rn. Note that because Q>0, the function f has a global minimizer that can be found by solving Qx=b.
Basic Conjugate Direction Algorithm
Given a starting point x(0) and Q-conjugate directions d(0),d(1),…,d(n−1); for k≥0,
g(k)αkx(k+1)=∇f(x(k))=Qx(k)−b,=−d(k)⊤Qd(k)g(k)⊤d(k),=x(k)+αkd(k). Theorem 1
For any starting point x(0), the basic conjugate direction algorithm converges to the unique x∗ (that solves Qx=b ) in n steps; that is, x(n)=x∗.
Proof
Consider x∗−x(0)∈Rn. Because the d(i) are linearly independent, there exist constants βi,i=0,…,n−1, such that
x∗−x(0)=β0d(0)+⋯+βn−1d(n−1). Now premultiply both sides of this equation by d(k)⊤Q,0≤k<n, to obtain
d(k)⊤Q(x∗−x(0))=βkd(k)⊤Qd(k), where the terms d(k)⊤Qd(i)=0,k=i, by the Q-conjugate property. Hence,
βk=d(k)⊤Qd(k)d(k)⊤Q(x∗−x(0)). Now, we can write
x(k)=x(0)+α0d(0)+⋯+αk−1d(k−1). Therefore,
x(k)−x(0)=α0d(0)+⋯+αk−1d(k−1). So writing
x∗−x(0)=(x∗−x(k))+(x(k)−x(0)) and premultiplying the above by d(k)⊤Q, we obtain
d(k)⊤Q(x∗−x(0))=d(k)⊤Q(x∗−x(k))=−d(k)⊤g(k), because g(k)=Qx(k)−b and Qx∗=b. Thus,
βk=−d(k)⊤Qd(k)d(k)⊤g(k)=αk and x∗=x(n), which completes the proof.
Lemma 2
In the conjugate direction algorithm,
g(k+1)⊤d(i)=0 for all k,0≤k≤n−1, and 0≤i≤k.
Proof
Note that
Q(x(k+1)−x(k))=Qx(k+1)−b−(Qx(k)−b)=g(k+1)−g(k), because g(k)=Qx(k)−b. Thus,
g(k+1)=g(k)+αkQd(k). We prove the lemma by induction. The result is true for k=0 because g(1)⊤d(0)=0, as shown before. We now show that if the result is true for k−1 (i.e., g(k)⊤d(i)=0,i≤k−1 ), then it is true for k (i.e., g(k+1)⊤d(i)=0, i≤k ). Fix k>0 and 0≤i<k. By the induction hypothesis, g(k)⊤d(i)=0. Because
g(k+1)=g(k)+αkQd(k), and d(k)⊤Qd(i)=0 by Q-conjugacy, we have
g(k+1)⊤d(i)=g(k)⊤d(i)+αkd(k)⊤Qd(i)=0. It remains to be shown that
g(k+1)⊤d(k)=0. Indeed,
g(k+1)⊤d(k)=(Qx(k+1)−b)⊤d(k)=(x(k)−d(k)⊤Qd(k)g(k)⊤d(k)d(k))⊤Qd(k)−b⊤d(k)=(Qx(k)−b)⊤d(k)−g(k)⊤d(k)=0, 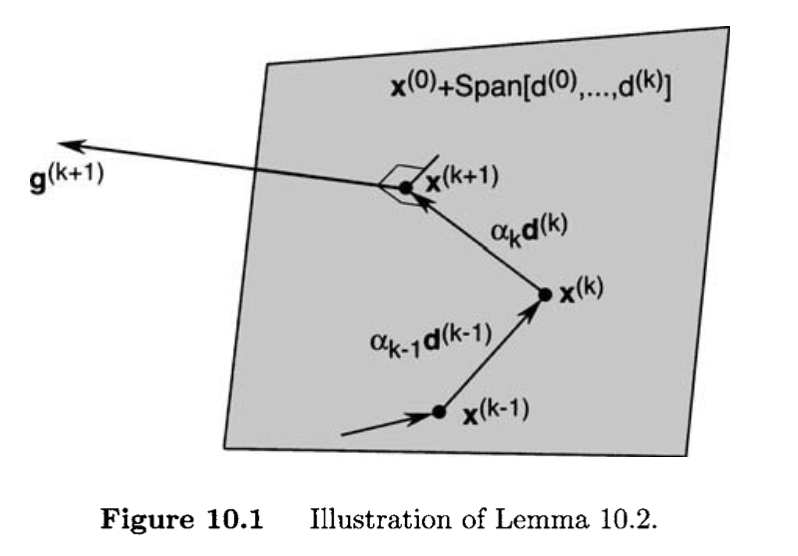
because Qx(k)−b=g(k).
Therefore, by induction, for all 0≤k≤n−1 and 0≤i≤k,
g(k+1)⊤d(i)=0. The Conjugate Gradient Algorithm
The conjugate gradient algorithm does not use prespecified conjugate directions, but instead computes the directions as the algorithm progresses. At each stage of the algorithm, the direction is calculated as a linear combination of the previous direction and the current gradient, in such a way that all the directions are mutually Q-conjugate - hence the name conjugate gradient algorithm. This calculation exploits the fact that for a quadratic function of n variables, we can locate the function minimizer by performing n searches along mutually conjugate directions.
As before, we consider the quadratic function
f(x)=21x⊤Qx−x⊤b,x∈Rn where Q=Q⊤>0. Our first search direction from an initial point x(0) is in the direction of steepest descent; that is,
d(0)=−g(0). Thus,
x(1)=x(0)+α0d(0), where
α0=α≥0argminf(x(0)+αd(0))=−d(0)⊤Qd(0)g(0)⊤d(0). In the next stage, we search in a direction d(1) that is Q-conjugate to d(0). We choose d(1) as a linear combination of g(1) and d(0). In general, at the (k+1) th step, we choose d(k+1) to be a linear combination of g(k+1) and d(k). Specifically, we choose
d(k+1)=−g(k+1)+βkd(k),k=0,1,2,… The coefficients βk,k=1,2,…, are chosen in such a way that d(k+1) is Q-conjugate to d(0),d(1),…,d(k). This is accomplished by choosing βk to be
βk=d(k)⊤Qd(k)g(k+1)⊤Qd(k). The conjugate gradient algorithm is summarized below.
- Set k:=0; select the initial point x(0).
- g(0)=∇f(x(0)). If g(0)=0, stop; else, set d(0)=−g(0).
- αk=−d(k)⊤Qd(k)g(k)⊤d(k).
- x(k+1)=x(k)+αkd(k).
- g(k+1)=∇f(x(k+1)). If g(k+1)=0, stop.
- βk=d(k)⊤Qd(k)g(k+1)⊤Qd(k).
- d(k+1)=−g(k+1)+βkd(k).
- Set k:=k+1; go to step 3.
Proposition
In the conjugate gradient algorithm, the directions d(0),d(1),…,d(n−1) are Q-conjugate.
Proof
We use induction. We first show that d(0)⊤Qd(1)=0. To this end we write
d(0)⊤Qd(1)=d(0)⊤Q(−g(1)+β0d(0)) Substituting for
β0=d(0)⊤Qd(0)g(1)⊤Qd(0) in the equation above, we see that d(0)⊤Qd(1)=0.
We now assume that d(0),d(1),…,d(k),k<n−1, are Q-conjugate directions. From Lemma 10.2 we have g(k+1)⊤d(j)=0,j=0,1,…,k. Thus, g(k+1) is orthogonal to each of the directions d(0),d(1),…,d(k). We now show that
g(k+1)⊤g(j)=0,j=0,1,…,k. Fix j∈{0,…,k}. We have
d(j)=−g(j)+βj−1d(j−1). Substituting this equation into the previous one yields
g(k+1)⊤d(j)=0=−g(k+1)⊤g(j)+βj−1g(k+1)⊤d(j−1) Because g(k+1)⊤d(j−1)=0, it follows that g(k+1)⊤g(j)=0.
We are now ready to show that d(k+1)⊤Qd(j)=0,j=0,…,k. We have
d(k+1)⊤Qd(j)=(−g(k+1)+βkd(k))⊤Qd(j). If j<k, then d(k)⊤Qd(j)=0, by virtue of the induction hypothesis. Hence, we have
d(k+1)⊤Qd(j)=−g(k+1)⊤Qd(j). But g(j+1)=g(j)+αjQd(j). Because g(k+1)⊤g(i)=0,i=0,…,k,
d(k+1)⊤Qd(j)=−g(k+1)⊤αj(g(j+1)−g(j))=0. Thus,
d(k+1)⊤Qd(j)=0,j=0,…,k−1. It remains to be shown that d(k+1)⊤Qd(k)=0. We have
d(k+1)⊤Qd(k)=(−g(k+1)+βkd(k))⊤Qd(k). Using the expression for βk, we get d(k+1)⊤Qd(k)=0, which completes the proof.
